Last Physics Engine Project

This is the last physics engine project. Your game design document will be due Friday @ 11:30pm this week. You can find a specification for the design document here.

Code Correctness

As always, this assignment has a particular set of design features that we expect you to focus on. This time, we will focus on testing; so, there are no new design features. Here’s the list of the other design features we’ve already highlighted:

encapsulation
code duplication
good variable and function names
procedural decomposition
“overcommenting” (e.g., the comments do not explain things that are already clear from the code itself)
usage of whitespace
overmodularization (e.g., modularizing into functions that actually make the code less clear)

Deliverables

This week’s demo is effectively an extension of last week’s with some minor changes. The two tasks this week are:

Implement collision resolution
Modify your Space Invaders game into a Breakout game

Demos

The main demo this week is a simple version of Breakout.

Your game demo must have the following features (but feel free to play around and implement anything you want otherwise):

There must be several rows of bricks that are rainbow colored
The ball must bounce off the paddle, the walls, the bricks (as well as destroy the bricks)
The game should reset when the player loses
You must include a “special feature” of your choice (power-ups, health on the bricks, etc.)

Additionally, we have provided you with a “pegs” demo which must work correctly with your code.

This week in particular, the demos may run slowly if compiled with asan. When you wish to run your demo, please run the command make NO_ASAN=true all, instead of the regular make all, or else you may experience demo slowdown.

Collision Resolution

Last week, you implemented find_collision() to detect collisions between two convex polygons. This week, you will implement collision resolution, which changes the velocities of the bodies based on the physics of the collision. There are two main components to implement:

Update find_collision() to return the direction along which the bodies are colliding
Write a force_creator_t that applies equal and opposite impulses to each body along the collision direction

Finding the collision axis

When two bodies collide in 3D space, there is a contact plane tangent to both bodies at the point of collision. The collision creates a “normal force” perpendicular to the contact plane. In 2D space, there is an analogous contact line tangent to the bodies. Just as in 3D physics, the applied force is perpendicular to the contact line. We refer to the unit vector perpendicular to the contact line as the “collision axis.” (There are actually two perpendicular directions; we will choose the one that points from the first body towards the second.) In the example below, the black line is the contact line and the red vector is the collision axis (from the green body towards the blue body).

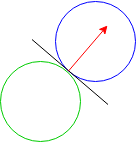
collision

When bodies are polygons rather than continuous shapes, there is no longer a tangent line, but we can approximate a collision axis.

If you implemented the Separating Axis method last week, the collision axis is simply the axis onto which the shapes’ projections have the least overlap.

Computing the impulse

You may remember from Ph 1a that when bodies collide, momentum is conserved. However, kinetic energy is only conserved when the bodies collide elastically (like billiard balls). You will implement collisions with variable amounts of elasticity, controlled by a parameter double elasticity. If elasticity is 1, the collision is elastic. If elasticity is 0, the collision is completely inelastic; if the bodies are moving along a line, they stick together when they collide. Values of elasticity between 0 and 1 correspond to partially elastic collisions. If elasticity is greater than 1, the collision is “super-elastic”: kinetic energy increases in the collision.

There is a simple formula for the impulse due to a collision with a certain elasticity, so we will apply impulses instead of forces to resolve the collision. The formula can be found on Wikipedia, but here’s an explanation:

Given that

m_a is the mass of the first body
m_b is the mass of the second body
u_a is the component of first body’s velocity along the collision axis (which points from the first body towards the second). Note that the component of a vector along a unit vector is just the dot product of the two vectors.
u_b is the component of the second body’s velocity along the collision axis (which points from the first body towards the second)
C_R is the coefficient of restitution, i.e. elasticity

The impulse applied to each body is parallel to the collision axis. The parallel component of the impulse applied to the first body is:

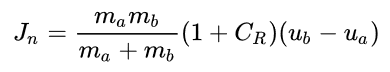
impulse

To conserve momentum, an equal and opposite impulse is applied to the second body.

Notes

Because bodies with mass INFINITY are not affected by forces or impulses, it is natural to use them as “walls” in a collision. For example, you could have implemented the bounce demo in project01 by making the star collide elastically with an infinite-mass wall on each side of the scene. This requires a minor change to the formula for computing the impulse: if one of the masses is INFINITY, the reduced mass (m_a * m_b / (m_a + m_b)) in the formula becomes the mass of the other body.

If two bodies collide in a tick and an impulse is applied to resolve the collision, they may still be colliding in the next tick. In this case, you should not apply a second impulse to the bodies in the next tick. Only resolve a collision between two bodies if they were not colliding in the previous tick.

Grading

The grading this week will be based on:

functionality
design