Collision Resolution

Last week, you implemented find_collision() to detect collisions between two convex polygons. This week, you will implement collision resolution, which changes the velocities of the bodies based on the physics of the collision. Here are your tasks for this week:

• Rewrite the destructive collision function and handler
• Update compare_collision() to return the direction along which the bodies are colliding
• Implement the physics collision handler

Finding the collision axis

When two bodies collide in 3D space, there is a contact plane tangent to both bodies at the point of collision. The collision creates a “normal force” perpendicular to the contact plane. In 2D space, there is an analogous contact line tangent to the bodies. Just as in 3D physics, the applied force is perpendicular to the contact line. We refer to the unit vector perpendicular to the contact line as the “collision axis.” (There are actually two perpendicular directions; we will choose the one that points from the first body towards the second.) In the example below, the black line is the contact line and the red vector is the collision axis (from the green body towards the blue body).

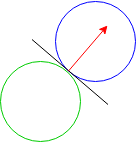
When bodies are polygons rather than continuous shapes, there is no longer a tangent line, but we can approximate a collision axis.

Since you implemented the Separating Axis method last week, the collision axis is simply the axis onto which the shapes’ projections have the least overlap.

Copying files Over

First, copy over the following library files from last week’s project:

• body.c
• list.c
• polygon.c
• vector.c
• scene.c

You may/may not also have to copy code from last week’s forces.c and forces.h if your teammates added helper functions/structs.

You will have to copy other files over as well, but they will be specified for you in the guide.

Collisions

We have added new collision functions for you in forces.h and forces.c. Like forces, collisions are “registered” in the scene using the create_x() x_force_creator() pattern. Take a look at them for more detail, and take note of the following things:

collision_aux_t

We’ve added a new collision_aux_t struct in forces.c that the new collision functions reference. Note that its structure is similar to that of body_aux_t with the exception of three additional fields:

• force_const: while this isn’t a new field, we wanted to make a note about this because force_const won’t necessarily be used by all collision force creators (destructive collisions are just one example). However, it will be used by some, and there’s another good reason why we include it that we’ll touch on later.
• handler: this is a collision handler that will run if a collision occurs between two bodies. Its type, collision_handler_t, has been defined for you in forces.h.
• aux: this void * field is for any extra information that the collision_aux_t will need access to. It’s a little bit meta and might be hard to wrap your head around at first, but this field will be especially helpeful when we need to reference variables like our state or scene. Again, this won’t necessarily be used by all collision handlers, especially if force_const can be used instead.

Finally, notice how we aren’t declaring a new collision_aux_free function. As of now, when the scene tries to free the force creator, it will use body_aux_free. Will that be a problem?

It actually won’t because of how we define collision_aux_t. Look at how the collision_aux_t struct is defined: the first two fields are the exact same as all the fields in body_aux_t. This allows casting the collision_aux_t to be casted as a body_aux_t, so body_aux_free will work as expected.

Furthermore, none of the other fields in collision_aux_t need to be freed. It could be argued that aux should be owned and freed by the collision_aux_t, but to keep only one free function, we’ll give the ownership of aux to the caller. At the end of the day, this is a design choice that we’ve made, and there’s not necessarily a “right” answer.

Given this information, your next task is rewrite create_destructive_collision after implementing destructive_collision.

Note that with the new abstraction that we’ve made for creating collisions, these two functions should be very short.

Collision Axis

First, take a look at collision.h. Since we care about the separating axis now, find_collision now returns a collision_info_t struct that contains whether or not the bodies collided in addition to the axis.

We’ve already rewritten find_collision to use the new return type of compare_collision. Take a look at it to see how compare_collision is supposed to interact with it.

Notice the double “overlap” variables. These variables represent the minimum overlap calculated by the two collision functions. We’ll pass in their addresses to compare_collision so that the function can update their values every time a new minimum overlap is found. If a collision has occurred, we’ll compare the minimum overlap from both calls and return the separating axis that corresponds to the smaller of the two.

Next, copy and paste your implementation of get_max_min_projections and compare_collision from last week into collision.c, taking care not to overwrite the collision_info_t return type. Here are the changes that you will have to make:

• keep track of the collision axis that corresponds to the minimum overlap
• instead of returning false, you’ll have to return a collision_info_t with that information. axis won’t have to be set to anything meaningful since we can assume that it won’t be accessed if a collision hasn’t occurred.
• calculate the overlap that occurs between the two projections. If the overlap is less than what min_overlap points to, update it along with the collision axis.
• If every projection overlaps, return the collision axis along with collision set to true.

Computing the impulse

This week, we’re also adding elastic collisions to our physics engine (specifically, in forces.c).

You may remember from Ph 1a that when bodies collide, momentum is conserved. However, kinetic energy is only conserved when the bodies collide elastically (like billiard balls). You will implement collisions with variable amounts of elasticity, controlled by a parameter double elasticity. If elasticity is 1, the collision is elastic. If elasticity is 0, the collision is completely inelastic; if the bodies are moving along a line, they stick together when they collide. Values of elasticity between 0 and 1 correspond to partially elastic collisions. If elasticity is greater than 1, the collision is “super-elastic”: kinetic energy increases in the collision.

There is a simple formula for the impulse due to a collision with a certain elasticity, so we will apply impulses instead of forces to resolve the collision. The formula can be found on Wikipedia, but here’s an explanation:

Given that

• m_a is the mass of the first body
• m_b is the mass of the second body
• u_a is the component of first body’s velocity along the collision axis (which points from the first body towards the second). Note that the component of a vector along a unit vector is just the dot product of the two vectors.
• u_b is the component of the second body’s velocity along the collision axis (which points from the first body towards the second)
• C_R is the coefficient of restitution, i.e. elasticity

The impulse applied to each body is parallel to the collision axis. The parallel component of the impulse applied to the first body is:

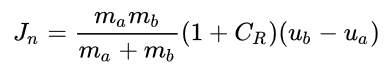
To conserve momentum, an equal and opposite impulse is applied to the second body. We have added this force_creator for you in forces.c.

Notes

Because bodies with mass INFINITY are not affected by forces or impulses, it is natural to use them as “walls” in a collision. For example, you could have implemented the bounce demo in project01 by making the star collide elastically with an infinite-mass wall on each side of the scene. This requires a minor change to the formula for computing the impulse: if one of the masses is INFINITY, the reduced mass (m_a * m_b / (m_a + m_b)) in the formula becomes the mass of the other body.

If two bodies collide in a tick and an impulse is applied to resolve the collision, they may still be colliding in the next tick. In this case, a second impulse should not be applied to the bodies in the next tick. A collision between two bodies will only be rsolved if they were not colliding in the previous tick. The logic for this has been implemented for you already in collision_force_creator.